Una sfera di massa 3.0×10−4 kg è sospesa a un filo. Una forza orizzontale costante la fa spostare in modo tale che il filo formi un angolo di 37° con la verticale. Trovare l’intensità della forza orizzontale e la tensione del filo.
Soluzione:
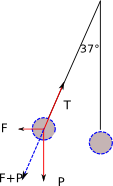
la sfera è vincolata, essendo sospesa ad un filo sicuramente fissato da qualche parte. La spinta della forza provocherà quindi una rotazione della sfera attorno a tale punto (come indicato in figura). Il peso della sfera è [ P=mg=3.0cdot10^{-4}, kgcdot9.8frac{m}{s^{2}}=2.9cdot10^{-3}, N ] Fintanto che la forza agisce, la sfera dovrebbe rimanere ferma nella posizione indicata; ciò implica che le forze agenti (peso, spinta orizzontale e tensione del filo) si equilibrano. Dalla figura si può osservare che se $$overrightarrow{F}+overrightarrow{P}=-overrightarrow{T}$$ allora la risultante è nulla. Calcoliamo la forza F, utilizzando i teoremi della trigonometria (il rapporto tra i due cateti è uguale alla tangente dell’angolo opposto al cateto al numeratore); sarà begin{eqnarray*} frac{overrightarrow{F}}{overrightarrow{P}}=tan37{^circ} & ; & overrightarrow{F}=2.9cdot10^{-3}, Ncdottan37{^circ}=2.2cdot10^{-3}, N end{eqnarray*} Mentre la tensione del filo è opposta alla somma di $overrightarrow{F}+overrightarrow{P}$ e quindi, applicando il th. di Pitagora, si ha [ overrightarrow{F}+overrightarrow{P}=-overrightarrow{T}=sqrt{left(2.9cdot10^{-3}, Nright)^{2}+left(2.2cdot10^{-3}, Nright)^{2}}=-3.6cdot10^{-3}, N ]
- Libro Fondamenti di Fisica Halliday