Un blocco di massa m=2.0 kg scorre su una superficie priva di attrito. A tale blocco è legato un blocco di massa M=4.0 kg con una fune tramite una puleggia. (fune e puleggia si intendono privi di massa e di attrito). Il moto è indicato dalle frecce. Quale dovrebbe essere la massa appesa per avere la massima accelerazione e quali saranno l’accelerazione e la tensione della fune corrispondente.
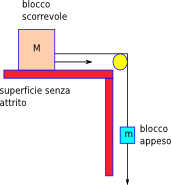
Soluzione:
l’accelerazione massima si ha scambiando il ruolo dei due corpi, quando la massa appesa è uguale a quella scorrevole; la forza che determina il moto del sistema è il peso del corpo appeso (la gravità sul blocco scorrevole, privo di attrito, non influisce sul moto). Per rispondere al secondo quesito, osserviamo che sul blocco scorrevole agiscono tre forze: la gravità, mg, la spinta del tavolo verso l’alto (reazione vincolare),?−?mg, e la tensione della fune, T diretta orizzontalmente; sul blocco appeso agiscono due forze, dirette verticalmente, ma di verso opposto: la gravità, ?−?Mg, e la tensione T della fune. Sul blocco scorrevole la somma di gravità e reazione vincolare è nulla ed agisce quindi solo la tensione T=Ma, diretta come la freccia in figura.
L’accelerazione e la tensione sono pertanto ottenibili risolvendo le due equazioni begin{eqnarray*} T-mg & = & -ma\ T & = & Ma end{eqnarray*} L’accelerazione si ottiene da [ Ma-mg+ma=0 ] risolvendo rispetto ad a, si ha [ a=left(frac{m}{M+m}right)g=frac{4, kg}{6, kg}cdot9.8,frac{m}{s^{2}}=6.5,frac{m}{s^{2}} ] la tensione sarà allora, sostituendo l’accelerazione a [ T=Ma=left(frac{Mm}{M+m}right)g=frac{2, kgcdot4, kgcdot9.8,frac{m}{s^{2}}}{6, kg}=13, N ]
- Libro Fondamenti di Fisica Halliday