Un corpo di massa 8.5 kg, può scorrere senza attrito su un piano inclinato di 30°. È tenuto in equilibrio tramite una fune un cui estremo è fissato ad una parete (si veda la figura). Trovare la tensione, T, della fune e la forza normale, N, che agisce sul blocco. Nel caso che la fune venga tranciata, trovare l’accelerazione del blocco.
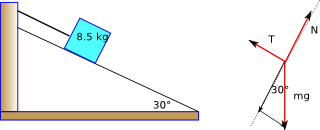
Soluzione:
Nel baricentro del blocco agiscono le tre forze indicate in figura; in particolare, mg è il peso del blocco, T< è la tensione della fune e N è la reazione vincolare . Se il corpo è inizialmente in equilibrio, la loro somma vettoriale deve essere nulla. Per eseguire questo calcolo, è necessario scomporre la forza peso nelle due componenti, mostrate in figura, dirette lungo il piano inclinato, come T e perpendicolarmente ad esso, come N. Il calcolo può essere fatto utilizzando le funzioni goniometriche, oppure, in questo caso, basta ricordare che un triangolo rettangolo con un angolo di 30° è la metà di un triangolo equilatero. Pertantobegin{eqnarray*} left(mgright)=P_{parallelo} & = & mgcdotfrac{1}{2}=frac{8.5, kgcdot9.8,frac{m}{s^{2}}}{2}=42, N\ left(mgright)=P_{perp} & = & mgcdotfrac{sqrt{3}}{2}=frac{8.5, kgcdot9.8,frac{m}{s^{2}}cdotsqrt{3}}{2}=72, N end{eqnarray*} Nella condizione di equilibrio si ha begin{eqnarray*} T & = & -P_{parallelo}=-42, N\ N & = & -P_{perp}=-72, N end{eqnarray*} Se la fune viene tranciata il corpo scende soggetto alla sola $P_{parallelo}$ e quindi con una accelerazione [ a=frac{P_{parallelo}}{m}=frac{-42}{8.5, kg}=4.9,frac{m}{s^{2}} ]
- Libro Fondamenti di Fisica Halliday