Se eseguiamo una divisione tra due numeri naturali sappiamo che non sempre otteniamo come risultato un numero naturale. Ad esempio, i risultati delle seguenti divisioni:
$$4:5quadquad 5:4quadquad 9:8$$
non sono dei numeri naturali bensì numeri decimali, infatti:
$$4:5=0,8quadquad 5:4=1,25quadquad 9:8=1,125$$
Consideriamo il seguente quesito: come dividere $4$ pani uguali tra $5$ persone? Ogni pane viene diviso in $5$ parti uguali in modo che ogni persona possa prenderne una fetta; così, la prima persona prende una fetta del primo pane, una del secondo, una del terzo e una del quarto.
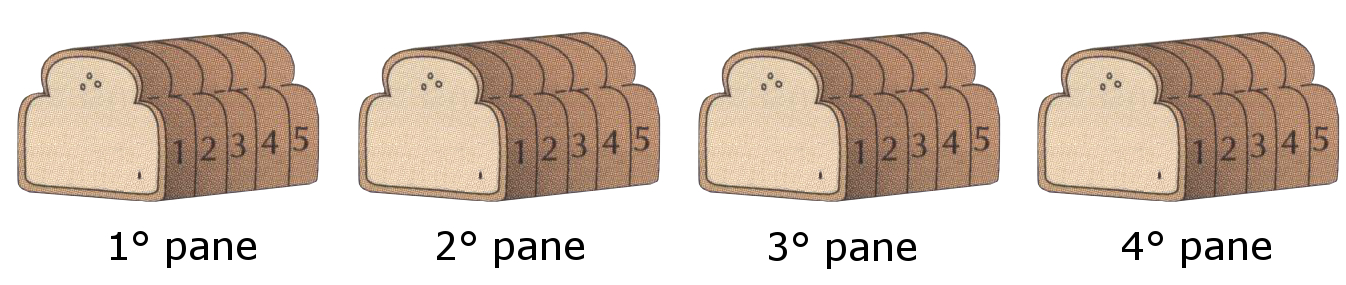
Ognuna delle $5$ parti uguali in cui è stato diviso un pane si dice "un quinto" e si indica con il simbolo $frac{1}{5}$.
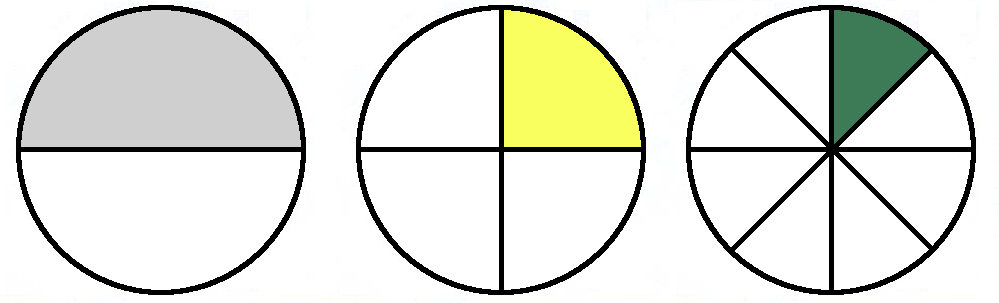
L'unità frazionaria $frac{1}{n}$ (con $nneq 0$) rappresenta una sola delle $n$ parti uguali in cui è stato diviso l'intero.
Ad esempio $frac{1}{2}, frac{1}{4}, frac{1}{8},dots$ sono unità frazionarie. Ognuna di esse indica che l'intero è stato diviso rispettivamente in $2, 4, 8$ parti e ne è stata considerata una.
Esempio Frazione 1
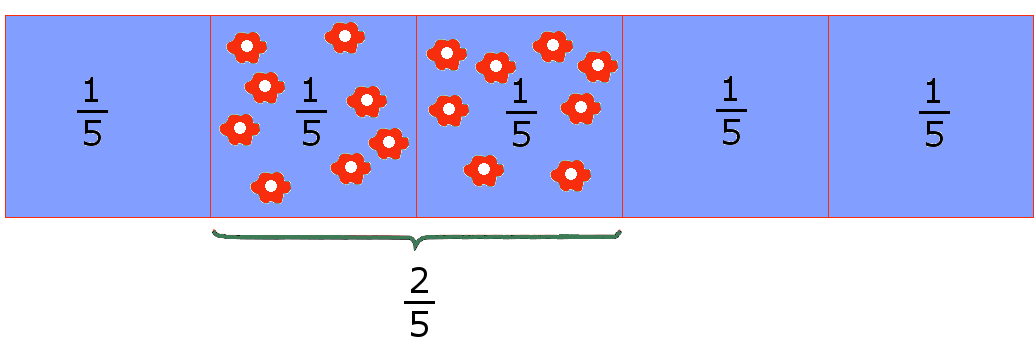
Se vogliamo tappezzare i $frac{2}{5}$ di una parete rettangolare, possiamo prima dividere la parete in $5$ parti uguali, ognuna delle quali vale $frac{1}{5}$ (unità frazionaria), e poi tappezzare due di queste parti
Esempio Frazione 2
Se vogliamo calcolare i $frac{3}{4}$ di $28$ alunni, possiamo prima calcolare quanti alunni corrispondono all'unità frazionaria $frac{1}{4}$, dividendo il numero degli alunni per $4$, e poi moltiplicare quest'ultimo valore per il numero $3$.
$$28 mbox{alunni}:4=7 mbox{alunni}quadquad 7 mbox{alunni}cdot 3=21 mbox{alunni}$$
Possiamo quindi concludere che i $frac{3}{4}$ di $28$ alunni corrispondono a $21$ alunni
In una frazione, come ad esempio $frac{2}{5}$, il $2$ è detto numeratore, il $5$ denominatore e la lineetta posta tra i due numeri di dice linea di frazione.

La frazione è un'operatore che divide l'intero in tante parti uguali, quante ne indica il denominatore, e ne prende in considerazione tante quante ne indica il numeratore
I problemi con le frazioni
Con gli strumenti a nostra disposizione siamo ora in grado di comprendere come una frazione operi su una grandezza.
Esempio
Spendiamo i $frac{2}{7}$ dei nostri risparmi, che ammontano a € $210$, per acquistare un lettore CD. Quanto abbiamo speso?
I dati del problema:
- $210=$ valore in Euro del totale dei risparmi; corrisponde all'intero
- Incognita: costo del lettore CD che corrisponde ai $frac{2}{7}$ dell'intero
Per la soluzione del problema rappresentiamo graficamente i dati:
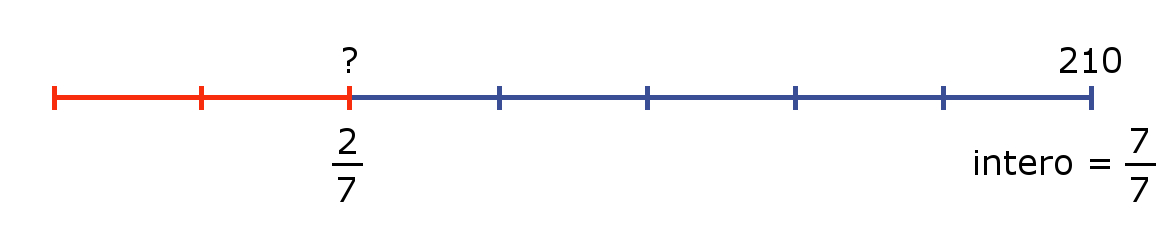
In questo caso il dato numerico ($210$) corrisponde all'intero. In base alla frazione unitaria che dobbiamo considerare$left(frac{1}{7}right)$ possiamo dire che $210$ corrisponde a $frac{7}{7}$. Per il calcolo dell'unità frazionaria basta allora svolgere la divisione:
$$210:7=30quad mbox{(valore in Euro della frazione unitaria $frac{1}{7}$ dell'intero)}$$
Per stabilire il prezzo del lettore CD basta osservare che tale quantità (in rosso) corrisponde a $2$ volte l'unità frazionaria cioè:
$$30cdot 2=60quad mbox{(valore in Euro del lettore CD cioè $frac{2}{7}$ dell'intero)}$$
Risposta: per l'aquisto del lettore CD abbiamo speso € $60$.
Esempio
Un ciclista percorre un tragitto lungo $675$ km in tre tappe. Il primo giorno percorre $frac{1}{3}$ dell'intero percorso; il secondo giorno i $frac{2}{5}$ dell'intero percorso. Calcoliamo quanti km ha percorso dopo il secondo giorno e quanti deve percorrerne nella terza tappa.
I dati del problema:
- $675=$ numero complessivo km del percorso
- $frac{1}{3} mbox{dell'intero} =$ prima tappa
- $frac{2}{5} mbox{dell'intero} =$ seconda tappa
- Incognite: numero km percorsi dopo il secondo giorno
numero km da percorrere nella terza tappa
In questo problema abbiamo due frazioni che si riferiscono allo stesso intero che è noto; la rappresentazione grafica dei dati del problema è la seguente:
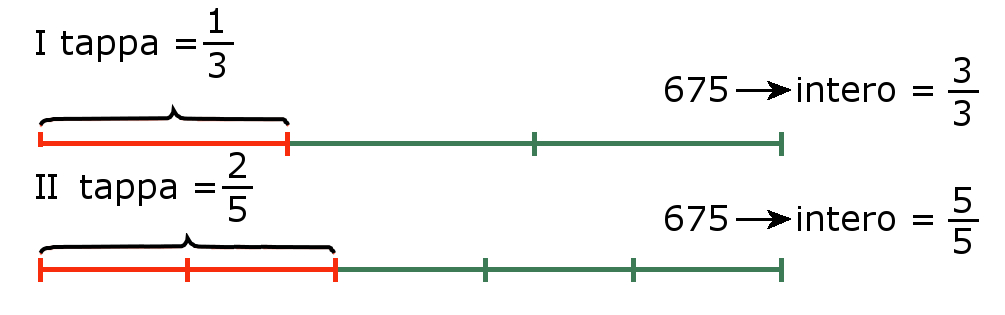
Per il calcolo della prima tappa dobbiamo svolgere l'operazione:
$$675:3=225quadmbox{(unità frazionaria della prima tappa in km $=frac{1}{3}$ dell'intero)}$$
Per il calcolo della seconda tappa dobbiamo osservare che l'unità frazionaria di riferimento cambia da $frac{1}{3}$ in $frac{1}{5}$, pertanto dobbiamo svolgere le seguenti operazioni:
$$675:5=135quadmbox{(unità frazionaria della seconda tappa in km $=frac{1}{5}$ dell'intero)}$$ $$135cdot 2= 270quadmbox{(seconda tappa in km $=frac{2}{5}$ dell'intero)}$$
Possiamo ora determinare le incognite del problema:
$$225+270=495quadmbox{(somma in km delle prime due tappe)}$$ $$675-495=180quadmbox{(terza tappa in km).}$$
Risolvi i seguenti problemi
- 1) Calcola i $frac{3}{5}$ di un segmento lungo $735$ cm.
- 2) In una scuola vi sono $300$ alunni. A quanti alunni corrispondono rispettivamente i $frac{3}{100}$, i $frac{3}{50}$ e i $frac{7}{60}$ dell'intera scuola?
- 3) Dopo aver letto i $frac{4}{9}$ delle pagine di un romanzo di avventura mi restano ancora da leggere $125$ pagine. Da quante pagine è costituito l'intero romanzo?
Classificazione delle frazioni
Le frazioni si classificano in:
- frazioni proprie
- frazioni improprie
- frazioni apparenti
Le frazioni proprie sono frazioni che hanno il numeratore minore del denominatore(ad esempio $frac{2}{3}$ e $frac{5}{6}$).
Le frazioni improprie sono frazioni che hanno il numeratore maggiore del denominatore(ad esempio $frac{8}{5}$ e $frac{6}{5}$).
Le frazioni apparenti sono frazioni che hanno il numeratore uguale o multiplo del denominatore(ad esempio $frac{3}{3}$ e $frac{8}{4}$).
Infine, due o più frazioni si dicono equivalenti se, operando sulla stessa grandezza, ne rappresentano una parte uguale.
Osserviamo, ad esempio, che le frazioni $frac{4}{6}$ e $frac{6}{9}$ si originano dalla frazione $frac{2}{3}$ moltiplicando contemporaneamente il numeratore e il denominatore di quest'ultima per una stessa quantità (rispettivamente per $2$ e per $3$):
$$frac{2}{3}=frac{2cdot 2}{3cdot 2}=frac{4}{6};quadquad frac{2}{3}=frac{2cdot 3}{3cdot 3}=frac{6}{9}.$$