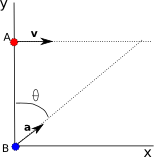
Una particella A si sposta sulla retta y=30 m a velocità costante di modulo v=3.0 m/s e direzione parallela all’asse x (si veda la figura). Una seconda particella B parte dall’origine, con velocità iniziale nulla e accelerazione di modulo a=0.40 m/s2, nello stesso istante in cui la particella A attraversa l’asse y. Quale angolo θ tra a e il verso positivo dell’asse y potrebbe provocare una collisione tra le due particelle?
Soluzione:
la particella A si muove in direzione orizzontale di moto rettilineo uniforme, mentre la particella B si muove di moto accelerato. La direzione del moto accelerato deve essere tale che le due particelle si incontrino. Pertanto, affinché B raggiunga A, è necessario che percorra una traiettoria scomponibile in un tratto orizzontale sxB=vt<=3.0t e un tratto verticale syB=30 m. La distanza complessiva che deve percorrere la particella B è descritta dal segmento obliquo in figura che è ottenibile applicando il th. di Pitagora al triangolo disegnato: [ s_{B}=sqrt{30^{2}+left(3tright)^{2}} ] tale distanza deve essere percorsa con una accelerazione a=0.4 m/s2 e partendo da ferma, per cui [ sqrt{30^{2}+left(3tright)^{2}}=frac{1}{2}at^{2}=0,2t^{2} ] Risolviamo elevando al quadrato [ 0,04t^{4}-9t^{2}-900=0 ] l’equazione è biquadratica e si risolve ponendo, ad es. t2=z [ 0,04z^{2}-9z-900=0 ] applicando la formula risolutiva, si ha, prendendo la sola soluzione positiva [ z=frac{9+sqrt{81+144}}{0.08}=300 ] risolviamo ora rispetto a t, considerando ancora la sola soluzione positiva per il tempo [ t=sqrt{300} ] Ora, l’angolo θ indicato in figura è legato alle due componenti dello spostamento dalla relazione [ tantheta=frac{s_{x}^{B}}{s_{y}^{B}}=frac{3t}{30} ] cioè, sostituendo il valore ottenuto per t [ theta=arctanleft(frac{3cdotsqrt{300}}{30}right)=60{^circ} ]
- Libro Fondamenti di Fisica Halliday