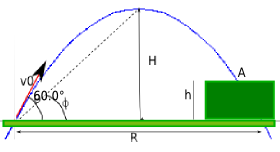
Una pietra viene proiettata verso un terrapieno di altezza h con la velocità iniziale di 42.0 m/s a un angolo di 60.0° rispetto al suolo orizzontale (vedi figura). La pietra cade in A, 5.50 s dopo il lancio. Trovare l’altezza h del terrapieno; la velocità della pietra subito prima dell’urto col terreno e la massima altezza H sopra il suolo raggiunto dalla pietra.
Soluzione:
utilizziamo la legge che descrive il moto parabolico della pietra. Nel tempo t=5.50 s, la pietra percorre in orizzontale la distanza [ x=v_{0}cosvartheta_{0}t=42.0,frac{m}{s}cdotcos60.0{^circ}cdot5.50, s=115.5, m ] e in verticale [ y=v_{0}sinvartheta_{0}t-frac{1}{2}gt^{2}=42.0,frac{m}{s}cdotsin60.0{^circ}cdot5.50, s-4.9,frac{m}{s^{2}}cdotleft(5.50,frac{m}{s}right)^{2}=51.8, m ] Prima dell’urto con il terrapieno la velocità si otterrà sommando vettorialmente la velocità orizzontale, costante, con quella diretta verticalmente begin{eqnarray*} v_{x} & = & v_{0}cosvartheta_{0}=42.0,frac{m}{s}cdotcos60.0{^circ}=21,frac{m}{s}\ v_{y} & = & v_{0}sinvartheta_{0}-gt=42.0,frac{m}{s}cdotsin60.0{^circ}-9.8,frac{m}{s^{2}}cdot5.50, s=-17.5,frac{m}{s} end{eqnarray*} la velocità sarà quindi [ v=sqrt{21^{2}+left(-17.5right)^{2}}=27.3,frac{m}{s} ] la massima altezza raggiunta è espressa da [ H=frac{v_{0}^{2}sin^{2}vartheta_{0}}{2g}=frac{left(42.0,frac{m}{s}right)^{2}sin^{2}60.0{^circ}}{2cdot9.8,frac{m}{s^{2}}}=67.5, m ]
- Libro Fondamenti di Fisica Halliday