Un aereo, picchiando a un angolo di 53° rispetto alla verticale, sgancia un proiettile a una quota di 730 m dal suolo. Il proiettile colpisce il terreno dopo 5.00 s. Trovare la velocità dell’aereo, la distanza orizzontale percorsa dal proiettile durante la caduta e infine le componenti orizzontale e verticale della sua velocità all’istante in cui ha colpito il terreno.
Soluzione:
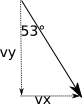
nell’istante in cui il proiettile viene sganciato la velocità dell’aereo e del proiettile solidale è quella illustrata in figura. Pertanto il proiettile, mentre percorre in caduta i 730 m, verrà accelerato verso il basso dal suo peso incrementando così la sua velocità verticale iniziale, secondo la legge del moto uniformemente accelerato [ s=v_{y}t+frac{1}{2}gt^{2} risolvendo rispetto a vy e sostituendo i valori assegnati, si ha [ v_{y}=frac{s-frac{1}{2}gt^{2}}{t}=frac{730, m-4.9,frac{m}{s^{2}}cdot5.00^{2}, s^{2}}{5.00, s}=121.5,frac{m}{s} ] diretta verso il basso; dalla componente verticale è possibile ottenere la velocità, attraverso i teoremi della trigonometria, cioè l’ipotenusa di un triangolo rettangolo è uguale al prodotto di un cateto per il coseno dell’angolo adiacente [ v=frac{121.5,frac{m}{s}}{cos53{^circ}}=202,frac{m}{s} ] É ora possibile calcolare anche la componente orizzontale del moto, anche col th. di Pitagora, [ v_{x}=sqrt{202^{2}-121.5^{2}}=161,frac{m}{s} ] Dalla componente orizzontale della velocità si ottiene la distanza orizzontale percorsa, in quanto tale moto può essere descritto dalle leggi del moto rettilineo uniforme [ x=v_{x}t=161,frac{m}{s}cdot5.00, s=806, m ] La componente orizzontale della velocità prima dell’impatto col terreno è sempre uguale a vx=161 m/s, mentre la componente verticale è quella ricavata pari a 121.5 m/s si ricava dalle leggi del moto accelerato [ v_{y}^{f}=v_{y}+gt=121.5,frac{m}{s}+9.81,frac{m}{s^{2}}cdot5, s=170.5,frac{m}{s} ] diretta verso il basso.
- Libro Fondamenti di Fisica Halliday