Se la posizione di una particella è data dalla funzione $$x=20t-50t^{3}$$ ove x è espresso in metri e t in secondi, dire (1) se, e quando, la velocità è nulla. (2) Quando è nulla l’accelerazione ? (3) Quando è negativa, quando positiva ? (4) Tracciare le curve x(t), v(t), a(t) della particella.
(1) ricavo la legge delle velocità, calcolando la derivata prima della legge oraria.begin{eqnarray*} v(t)=20-15t^{2}=0 & t=sqrt{frac{4}{3}}simeq & 1.2, s end{eqnarray*} considerando solo la soluzione positiva dell’equazione di secondo grado.
(2) ricavo l’accelerazione in funzione del tempo, sempre calcolando la derivata prima della legge delle velocità: begin{eqnarray*} a(t)=-30t=0 & & t=0 end{eqnarray*}
(3) dall’equazione precedente, a(t)=-30t, si ottiene a>0 per t<0 e a<0 per t>0
(4)
• curva x(t): polinomiale di terzo grado ?
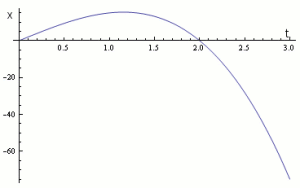
• curva v(t): polinomiale di secondo grado, parabola?
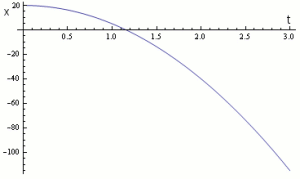
• curva a(t): funzione lineare, retta?
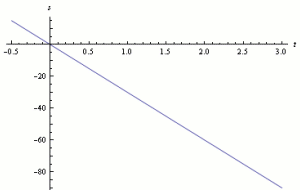
- Libro Fondamenti di Fisica Halliday