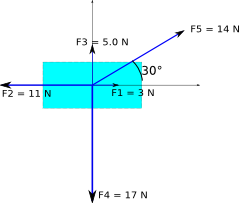
Cinque forze agiscono sulla scatola in figura di massa 2.0 kg. Trovare la sua accelerazione nella sua notazione vettoriale e in intensità e direzione.
Soluzione:
L’accelerazione ha la stessa direzione della forza risultante. Calcoliamo prima la forza risultante dalla somma delle cinque forze assegnate. Esprimiamo le cinque forze secondo le loro componenti lungo gli assi coordinati [ begin{array}{ccc} F_{1} & = & 3.0vec{i}\ F_{2} & = & -11vec{i}\ F_{3} & = & 5.0vec{j}\ F_{4} & = & -17vec{j}\ F_{5} & = & 12.1vec{i}+7.0vec{j} end{array} ] La risultante sarà pertanto [ overrightarrow{R}=left(3.0-11+12.1right)vec{i}+left(5.0-17+7.0right)vec{j}=4.1vec{i}-5.0vec{j} ] La forza risultante ha intensità [ R=sqrt{4.1^{2}+left(-5.0right)^{2}}=6.5, N ] formante un angolo $$alpha=arctanleft(frac{-5.0}{4.1}right)=-50{^circ}$$ con l’asse orizzontale. L’accelerazione ha la stessa direzione della forza intensità [ a=frac{F}{m}=frac{6.5}{2.0}=3.25,frac{m}{s^{2}} ] Le sue componenti saranno [ begin{array}{ccc} a_{x} & = & 3.25cdotcosleft(-50{^circ}right)=2.0\ a_{y} & = & 3.25cdotsinleft(-50{^circ}right)=-2.5 end{array} ] da cui [ overrightarrow{a}=2.0overrightarrow{i}-2.5overrightarrow{j} ]
- Libro Fondamenti di Fisica Halliday