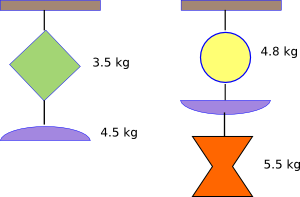
Un oggetto da ornamento sospeso al soffitto è formato da due pezzi di metallo, uniti da fili di massa trascurabile, le cui masse sono quelle indicate in figura. Determinare la tensione nel filo inferiore e in quello superiore. Se si aggiunge, in figura a destra, un terzo pezzo metallico, sapendo che la tensione nel filo più in alto è di 199 N, trovare la tensione nel filo di mezzo e in quello in basso.
Soluzione:
la figura indica le masse che sono soggette ad una accelerazione di gravità di 9.8 m/s2; il filo agganciato al soffitto, rappresenta il vincolo che impedisce all’oggetto di cadere; il primo tratto di filo sopporta il peso di entrambi i due pezzi, la cui massa complessiva è $$m=m_{1}+m_{2}=3.5, kg+4.5, kg=8, kg$$ la tensione sarà quindi [ T_{sup}=8, kgcdot9.8,frac{m}{s^{2}}=78, N ] la parte inferiore sostiene solo il secondo pezzo di massa m2=4.5 kg, pertanto[ T_{inf}=4.5, kgcdot9.8,frac{m}{s^{2}}=44, N ] Nel secondo caso, con i tre pezzi, è nota la tensione del filo più alto, cioè quello che deve sostenere le tre masse; è quindi possibile ricavare la massa del terzo pezzo; da [ T_{sup}=left(m_{1}+m_{2}+m_{3}right)g=left(10.3+m_{2}right)g ] si ha [ m_{2}=frac{T_{sup}}{g}-10.3=frac{199, N}{9.8,frac{m}{s^{2}}}-10.3, kg=10, kg ] La tensione del filo centrale, che deve sostenere due pezzi, sarà [ T_{cent}=left(10+5.5right)kgcdot9.8,frac{m}{s^{2}}=152, N ] La tensione del filo inferiore, che deve sostenere solo un pezzo, sarà [ T_{cent}=5.5, kgcdot9.8,frac{m}{s^{2}}=54, N ]
- Libro Fondamenti di Fisica Halliday