$\{(x^2-49>0),((x^2)/3-27>=0):}$

A cura di: Francesco Speciale

${(x^2-49>0),((x^2)/3-27>=0):}$

---

 

${(x^2-49>0),((x^2)/3-27>=0):}$;
${(x^2>49),((x^2)/3>=27):}$;
Studiamo le due disequazioni singolarmente

1)$x^2>49$

Siccome il coefficiente di $x^2$ e il segno della disequazione sono concordi,
prenderemo come soluzione accettabile l’intervallo esterno, per cui la soluzione sarà:
$x<-7 vv x>7$.

2)$(x^2)/3>=27 => x^2>=81$

Siccome il coefficiente di $x^2$ e il segno della disequazione sono concordi,
prenderemo come soluzione accettabile l’intervallo esterno, per cui la soluzione sarà:
$x<=-9 vv x>=9$.

Pertanto
${(x<-7 vv x>7),(x<=-9 vv x>=9):}$;
Soluzione del sistema sarà l’intersezione delle singole soluzioni delle disequazioni che lo compongono.

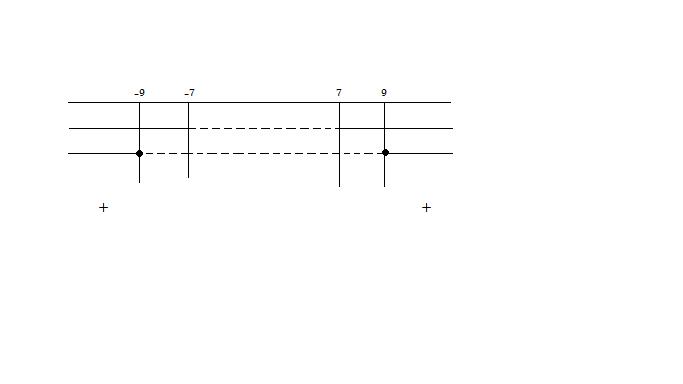
Quindi la soluzione sarà:$x<=-9 vv x>=9$.