A cura di: Francesco Speciale
Risolvere il seguente triangolo rettangolo $(alpha=90^circ)$
$b=10sqrt3; c=10$
In questo caso ci è noto la misura del cateto minore e del cateto maggiore, oltre all’angolo retto $alpha=90^circ$.
Per definizione noi sappiamo che $tg(beta)=b/c=(10sqrt3)/(10)=sqrt3$
quindi $beta=arctg(sqrt3)=30^circ$
Quindi poichè la somma degli angoli interni di un triangolo è di $180^circ$, ovvero
$alpha+beta+gamma=180^circ$
si ha che
$90^circ+30^circ+gamma=180^circ => gamma=180^circ-90^circ-30^circ=60^circ$.
Pertanto $gamma=60^circ$.
In un triangolo rettangolo un cateto è uguale al prodotto dell’ipotenusa
per il seno dell’angolo opposto al cateto stesso
$b=asin(beta) => a=b/(sin(beta))=(10)/(sin(30^circ))=(10)/(1/2)=20$;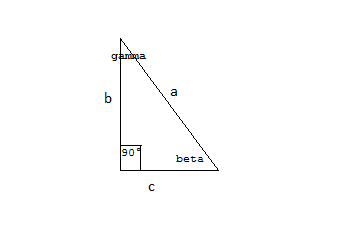
- Trigonometria