Equilibrio statico e dinamico: definizione ed esercizi svolti

EQUILIBRIO STATICO E DINAMICO

Ecco il riassunto su equilibrio statico e dinamico in fisica, insieme ad esercizi svolti come esempio.

EQUILIBRIO STATICO E DINAMICO: DEFINIZIONE E SPIEGAZIONE

Capire il significato di equilibrio statico e dinamico è importante in fisica, perché ci permette di verificare lo stato di quiete di un corpo o se esso si muove di moto uniforme. Andiamo a vedere nel dettaglio cosa vuol dire per un corpo soggetto a forze esterne essere in equilibrio statico o dinamico.

In pratica se noi abbiamo un corpo, per esempio una bacchetta, su cui agiscono delle forze dobbiamo verificare innanzi tutto se la sommatoria di tutte le forze (nonché dei momenti) che agiscono su di essa è nulla. Secondariamente dobbiamo costatare se il corpo ha velocità nulla o diversa da zero.

Se sul corpo abbiamo sommatoria delle forze, dei momenti pari a zero e velocità nulle, allora possiamo affermare che il corpo è in equilibrio statico. In formule:

∑ F = 0

∑ M = 0

v = 0

ω = 0     (velocità angolare)
 

Se sul corpo abbiamo sommatoria delle forze, dei momenti pari a zero e si muove di moto uniforme (ovvero accelerazione pari a zero), allora possiamo affermare che il corpo è in equilibrio dinamico. In formule:

(accelerazione angolare)

Quindi se su un corpo esistono le condizioni sopra elencate: ogni corpo persevera nel suo stato di quiete o di moto rettilineo uniforme, se qualche forza (squilibrata) ad esso applicata non lo costringe a mutarlo. Questo è la Prima legge della dinamica o Principio d’inerzia.
 

EQUILIBRIO STATICO E DINAMICO FISICA: ESERCIZI

Immaginiamo di avere un dondolo costituito da una tavola di lunghezza 3,6 m poggiata su un supporto (posto al centro) come in figura:

 

 

Il primo bambino (freccia verde), che ha una massa di 35 Kg, si siede ad una delle estremità del dondolo. A che distanza si deve sedere la bambina (freccia gialla) in modo da equilibrare il dondolo se ha una massa di 50 Kg? E la forza che deve esercitare il supporto quando vale?

Dati:
m₁ = 35 Kg ;  m₂ = 50 Kg ;  L = 3,6 m.

Con b₁ e b₂ indichiamo le distanze dal fulcro dei due bambini, mentre con H la forza che deve esercitare il supporto.

Sapendo che il primo bambino si posiziona all’estremità del dondolo allora

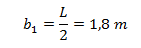
Sfruttando il fatto che la sommatoria dei momenti deve essere pari a zero possiamo trovare b₂ 

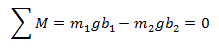
Quindi

m₁gb₁ = m₂ gb₂

Da cui ricaviamo

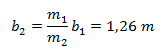
Mentre se sfruttiamo l’equazione sulle forze possiamo trovare la forza che deve esercitare il supporto

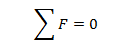
Considerando il verso delle forze abbiamo le due forze peso verso il basso (per convenzione prendiamo il segno +) e quella del supporto verso l’alto (con segno a questo punto negativo), quindi

m₁ g + m₂ g – H = 0

Da cui ricaviamo H

H = g(m₁ + m₂) = 833,85 N

La forza esercitata dal supporto sarà pari alla somma delle forze peso, ma con verso opposto, ovviamente.

Ti servono altri appunti, riassunti o temi svolti? Ti aiutiamo noi!
Iscriviti al gruppo: Sos Compiti: riassunti e temi svolti e non perderti le nostre risorse utili sulla meccanica.