Tre astronauti, muniti di zaino a razzo, spingono e guidano un asteroide di 120 kg esercitando le forze indicate in figura. Trovare l’accelerazione dell’asteroide in notazione per vettori unitari e in intensità e direzione.
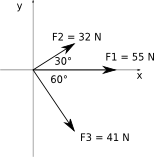
Soluzione:
esercizio un poco fantascientifico. In ogni caso, per determinare l’accelerazione è necessario conoscere la forza risultante. Trattandosi di angoli di 30° e 60°, cioè angoli che si riferiscono a triangoli equilateri e alle loro metà, è possibile calcolare le componenti verticali ed orizzontali delle forze anche senza l’ausilio delle funzioni goniometriche. [ begin{array}{cccccccc} F_{1x} & = & 55, N & & & F_{1y} & = & 0\ F_{2x} & = & 27.7, N & & & F_{2y} & = & 16, N\ F_{3x} & = & 20.5, N & & & F_{3y} & = & -35.5, N end{array} ] La risultante sarà pertanto [ overrightarrow{R}=left(55+27.7+20.5right)overrightarrow{i}+left(16-35.5right)overrightarrow{j}=103.2overrightarrow{i}-19.5overrightarrow{j} ] L’accelerazione sarà data da [ overrightarrow{a}=frac{overrightarrow{R}}{m}=0.86overrightarrow{i}-0.16overrightarrow{j} ] l’intensità dell’accelerazione sarà [ a=sqrt{0.86^{2}+left(-0.16right)^{2}}=0.87,frac{m}{s^{2}} ] la direzione [ alpha=arctanfrac{-0.16}{0.86}=-10.5{^circ} ]
- Libro Fondamenti di Fisica Halliday



