$|x^2-9x+15|>1$

A cura di: Francesco Speciale

$|x^2-9x+15|>1$

---

$|x^2-9x+15|>1$
La disequazione è equivalente alle due disequazioni: $x^2-9x+15>1 vv x^2-9x+15<-1$.
che possiamo mettere a sistema
${(x^2-9x+15>1),(x^2-9x+15<-1):}$;

Risolviamo il seguente sistema
${(x^2-9x+15>1),(x^2-9x+15<-1):}$;
${(x^2-9x+14>0),(x^2-9x+16<0):}$;
Studiamo singolarmente le due disequazioni
1)$x^2-9x+14>0$

$Delta=b^2-4ac=(-9)^2-(4*14*1)=81-56=25$
$x_(1,2)=(-b+-sqrt(Delta))/(2a)=(9+-sqrt(25))/2=(9+-5)/2 => x_1=2 ^^ x_2=7$.

Siccome il coefficiente di $x^2$ e il segno della disequazione sono concordi,
prenderemo come soluzione accettabile l’intervallo esterno,
per cui la soluzione sarà:
$x<2 vv x>7$.

2)$x^2-9x+16<0$

$Delta=b^2-4ac=(-9)^2-(4*16*1)=81-64=17$
$x_(1,2)=(-b+-sqrt(Delta))/(2a)=(9+-sqrt(17))/2 => x_1=(9+sqrt(17))/2 ^^ x_2=(9-sqrt(17))/2$.

Siccome il coefficiente di $x^2$ e il segno della disequazione sono discordi,
prenderemo come soluzione accettabile l’intervallo interno,
per cui la soluzione sarà:
$(9-sqrt(17))/2<x<(9+sqrt(17))/2$.
Poichè dobbiamo considerare l’unione delle due soluzioni, si ha

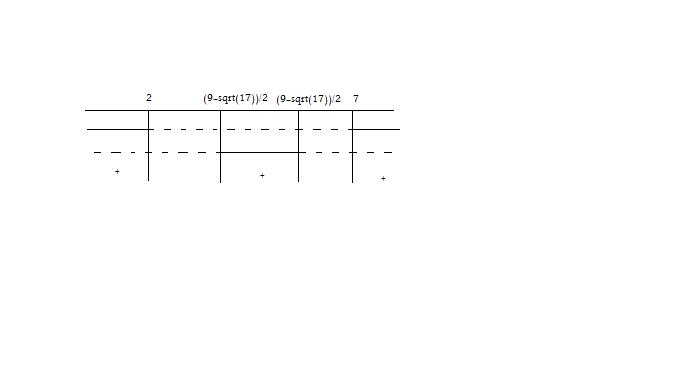
Pertanto la disequazione è verificata per $x<2 vv (9-sqrt(17))/2<x<(9+sqrt(17))/2 vv x>7$.