Determinare l’accelerazione centripeta dovuta alla rotazione della Terra per un oggetto che si trova sull’equatore. Quale dovrebbe essere il periodo di rotazione della Terra affinché questa accelerazione sia uguale a 9.8 m/s2? Calcolare infine l’accelerazione per una persona posta ad una latitudine di 40° N.
Soluzione:
assumendo il raggio terrestre di 6.37×106 m e poiché l’equatore è un cerchio massimo, si ha [ a=frac{v^{2}}{r}=frac{left(frac{2pi r}{T}right)^{2}}{r}=frac{4pi^{2}r}{T^{2}} ] ora sapendo che il periodo di rotazione corrisponde ad un giorno che contiene T=24×3600 s, si ha a=frac{4pi^{2}cdot6.37cdot10^{6}, m}{86400^{2}, s^{2}}=0.034,frac{m}{s^{2}} ] per avere una accelerazione pari a quella di gravità, il periodo dovrebbe essere [ T=sqrt{frac{4pi^{2}r}{a}}=sqrt{frac{4pi^{2}cdot6.37cdot10^{6}, m}{9.8,frac{m}{s^{2}}}}=5066, s=84.4, minuti ] Se la persona è posta alla latitudine di 40° N, descrive un cerchio (parallelo) più piccolo (si veda una rappresentazione schematica in figura).
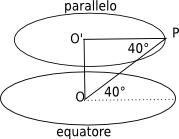
Applicando il teorema dei triangoli rettangoli a PO’O, si ha [ PO’=r_{parallelo}=OPcos40{^circ}=6.37cdot10^{6}, mcdotcos40{^circ}=4.88cdot10^{6}, m ] Applicando la relazione scritta sopra, con periodo uguale (la velocità angolare della Terra è sempre la stessa), si ha [ a=frac{4pi^{2}cdot4.88cdot10^{6}, m}{86400^{2}, s^{2}}=0.026,frac{m}{s^{2}} ]