Dimostrare che, per un proiettile sparato da un terreno piano a un angolo θ0 rispetto all’orizzontale, il rapporto fra la massima altezza H e la gittata R è dato dall’espressione $$H/R=frac{1}{4}tanvartheta_{0}$$ Per quale angolo si ha H=R?
Soluzione:
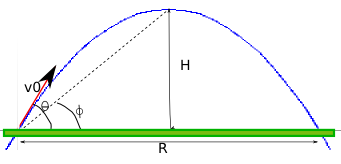
La relazione che esprime il punto di massima altezza, cioè il punto in cui vy=v0sin ϑ0=0, è [ H=frac{v_{0}^{2}sin^{2}vartheta_{0}}{2g} ] mentre la gittata, distanza tra punto di partenza e di ricaduta, cioè nel modello geometrico la distanza tra le intersezioni della parabola con l’asse orizzontale, è espressa da [ R=frac{v_{0}^{2}sin2vartheta_{0}}{g}=frac{2v_{0}^{2}sinvartheta_{0}cosvartheta_{0}}{g} ] il loro rapporto sarà pertanto [ frac{H}{R}=frac{frac{v_{0}^{2}sin^{2}vartheta_{0}}{2g}}{frac{2v_{0}^{2}sinvartheta_{0}cosvartheta_{0}}{g}}=frac{v_{0}^{2}sin^{2}vartheta_{0}}{2g}cdotfrac{g}{2v_{0}^{2}sinvartheta_{0}cosvartheta_{0}}=frac{1}{4}tanvartheta_{0} ] Se H=R, allora il rapporto H, cioè $$frac{1}{4}tanvartheta_{0}=1$$ Risolvendo la equazione goniometrica elementare, si ha [ vartheta_{0}=arctan4=76{^circ} ]