Una bolla d’aria con un volume di 20cm3 si trova sul fondo di un lago profondo 40m dove la temperatura è 4,0°C. La bolla sale in superficie, dove la temperatura è di 20°C. Supponete che la temperatura della bolla sia la stessa dell’acqua circostante e trovate il suo volume appena prima che raggiunga la superficie.
Risoluzione
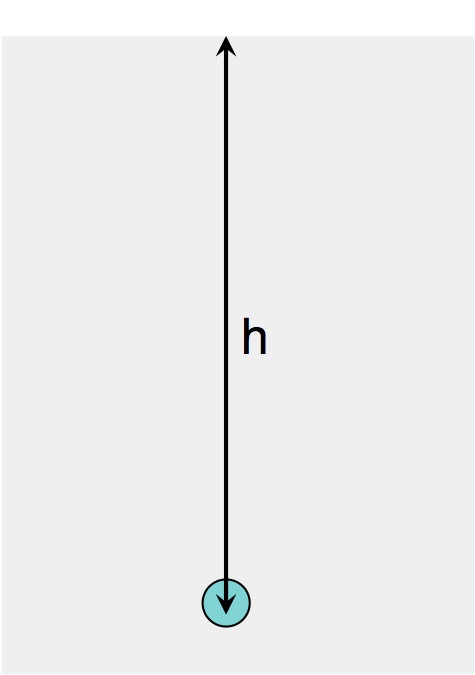
1) Alla profondità h=40m la pressione dell’aria nella bolla è pari alla pressione esterna esercitata dall’acqua sulla bolla:
[{{rm{p}}_{rm{1}}} = {{rm{p}}_{rm{0}}} + rho {rm{gh}} = {rm{4,93}} cdot {rm{1}}{{rm{0}}^{rm{5}}}{rm{Pa}}]
dove p0=1,01·105 Pa è la pressione atmosferica e ρ=1000kg/m3 è la densità dell’acqua
2) Applicando l’equazione di stato dei gas perfetti quando la bolla è a profondità h, dove p=p1, V=V1=20·10-6m3 e T=T1=277K, possiamo calcolare il numero di moli di aria:
[{{rm{p}}_{rm{1}}}{{rm{V}}_{rm{1}}} = {rm{nR}}{{rm{T}}_{rm{1}}} Rightarrow {rm{n}} = frac{{{{rm{p}}_{rm{1}}}{{rm{V}}_{rm{1}}}}}{{{rm{R}}{{rm{T}}_{rm{1}}}}} = {rm{4,28}} cdot {rm{1}}{{rm{0}}^{ – {rm{3}}}}{rm{moli}}]
3) Sulla superficie del lago la pressione dell’aria sarà p2=p0 (pressione atmosferica) . Applicando l’equazione di stato dei gas perfetti quando la bolla è in superficie, alla pressione p2 e alla temperatura T2=293K possiamo calcolare il volume finale V2 della bolla:
[{{rm{p}}_{rm{2}}}{{rm{V}}_{rm{2}}} = {rm{nR}}{{rm{T}}_{rm{2}}} Rightarrow {{rm{V}}_{rm{2}}} = frac{{{rm{nR}}{{rm{T}}_{rm{2}}}}}{{{{rm{p}}_{rm{2}}}}} = {rm{1,03}} cdot {rm{1}}{{rm{0}}^{ – {rm{4}}}}{{rm{m}}^{rm{3}}} = {rm{103c}}{{rm{m}}^{rm{3}}}]