Libro Fondamenti di Fisica Halliday - Capitolo 20 Problema 25

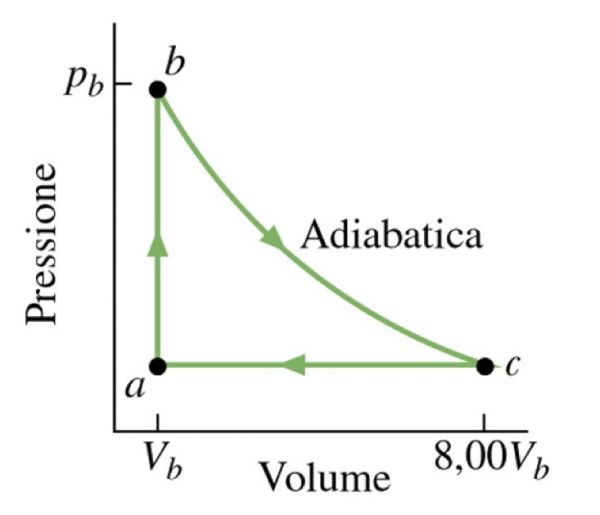
A 1,00mol di un gas ideale monoatomico viene fatto percorrere il ciclo mostrato in figura. Il processo bc è un’espansione adiabatica (p_b=10,1bar, V_b=1,00×10^-3m³). Si calcoli per ogni ciclo il calore fornito al gas, il calore restituito dal gas, il lavoro totale compiuto dal gas e il rendimento.

Risoluzione

Nel punto B si ha p_b=10,1×105Pa e V_b=1,00×10^-3m₃. Applicando l’equazione dei gas ideali si ha:

[{{rm{p}}_{rm{b}}}{{rm{V}}_{rm{b}}} = {rm{nR}}{{rm{T}}_{rm{b}}} Rightarrow {{rm{T}}_{rm{b}}} = frac{{{{rm{p}}_{rm{b}}}{{rm{V}}_{rm{b}}}}}{{{rm{nR}}}} = {rm{122K}}]

Nel punto c sappiamo che V_c=8,00V_b=8,00m³. Dall’equazione della trasformazione adiabatica BC si ha:

[{{rm{T}}_{rm{b}}}{rm{V}}_{rm{b}}^{gamma {rm{ – 1}}} = {{rm{T}}_{rm{c}}}{rm{V}}_{rm{c}}^{gamma {rm{ – 1}}} Rightarrow {{rm{T}}_{rm{c}}} = {{rm{T}}_{rm{b}}}{left( {frac{{{{rm{V}}_{rm{c}}}}}{{{{rm{V}}_{rm{b}}}}}} right)^{gamma  – {rm{1}}}} = {rm{30,5K}}]

Applicando poi l’equazione di stato dei gas perfetti nel punto C:

[{{rm{p}}_{rm{c}}}{{rm{V}}_{rm{c}}} = {rm{nR}}{{rm{T}}_{rm{c}}} Rightarrow {{rm{p}}_{rm{c}}} = frac{{{rm{nR}}{{rm{T}}_{rm{c}}}}}{{{{rm{V}}_{rm{c}}}}} = {rm{3,17}} times {rm{1}}{{rm{0}}^{rm{4}}}{rm{Pa}}]

Nel punto A p_a=pc=3,17×10⁵Pa e V_a=V_b=10^-3m³. Per cu si ha:

[{{rm{p}}_{rm{a}}}{{rm{V}}_{rm{a}}} = {rm{nR}}{{rm{T}}_{rm{a}}} Rightarrow {{rm{T}}_{rm{a}}} = frac{{{{rm{p}}_{rm{a}}}{{rm{V}}_{rm{a}}}}}{{{rm{nR}}}} = {rm{3,81K}}]

 

Calcoliamo ora i calori scambiati dal gas nel ciclo:

[{{rm{Q}}_{{rm{ab}}}} = {rm{n}}{{rm{C}}_{rm{V}}}left( {{{rm{T}}_{rm{b}}} – {{rm{T}}_{rm{a}}}} right) = frac{{rm{3}}}{{rm{2}}}{rm{nR}}left( {{{rm{T}}_{rm{b}}} – {{rm{T}}_{rm{a}}}} right) = {rm{1470J}}]

[{{rm{Q}}_{{rm{bc}}}} = {rm{0}}]

[{{rm{Q}}_{{rm{ca}}}} = {rm{n}}{{rm{C}}_{rm{P}}}left( {{{rm{T}}_{rm{a}}} – {{rm{T}}_{rm{c}}}} right) = frac{{rm{5}}}{{rm{2}}}{rm{nR}}left( {{{rm{T}}_{rm{a}}} – {{rm{T}}_{rm{c}}}} right) =  – {rm{554J}}]

In un ciclo ΔE_int=0 e quindi Q=L:

[{rm{L}} = {{rm{Q}}_{{rm{ab}}}} + {{rm{Q}}_{{rm{bc}}}} + {{rm{Q}}_{{rm{ca}}}} = {rm{916J}}]

Il rendimento è dato da:

[eta  = frac{{rm{L}}}{{{{rm{Q}}_{}}}} = frac{{rm{L}}}{{{{rm{Q}}_{{rm{AB}}}}}} = {rm{0,623}}]