A cura di: Francesco Speciale
Verificare che il quadrangolo di vertici $A(2;2); B(8;2); C(10;5); D(4;5)$ è un parallelogrammo.
Svolgimento
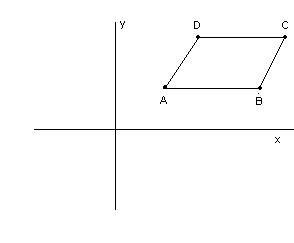
Per dimostrare che il quadrangolo ottenuto è un parallelogrammo basta verificare che i lati opposti sono uguali, cioè
$bar(AB)=bar(DC) ^^ bar(BC)=bar(AD)$.
Calcoliamo il segmento $bar(AB)$
Possiamo notare che il segmento $bar(AB)$ è parallello all’asse delle ascisse,
cioè $y_1=y_2=2$.
Pertanto la loro distanza è il valore assoluto della differenza delle loro ascisse
$d=|x_2-x_1|=|8-2|=|6|=6$.
Calcoliamo $bar{DC}$
Possiamo notare che il segmento $bar(DC)$ è parallello all’asse delle ascisse,
cioè $y_3=y_4=5$.
Pertanto la loro distanza è il valore assoluto della differenza delle loro ascisse
$d=|x_4-x_3|=|4-10|=|-6|=6$.
Quindi $bar(AB)=bar(DC)$
Calcoliamo ora $bar(AD)$ e $bar(BC)$
$bar(AD)=sqrt((x_4-x_1)^2+(y_4-y_1)^2)=sqrt((4-2)^2+(5-2)^2)=sqrt(4+9)=sqrt(13)$
$bar(BC)=sqrt((x_3-x_2)^2+(y_3-y_2)^2)=sqrt((10-8)^2+(5-2)^2)=sqrt(4+9)=sqrt(13)$
Quindi $bar(AD)=bar(BC)$.
Pertanto abbiamo verificato che il quadrangolo di vertici $A(2;2); B(8;2); C(10;5); D(4;5)$ è un parallelogrammo.


